Solving the Square Dance
I've since found a better solution to this awesome problem, but, for history's sake, you can look at this one if you want.
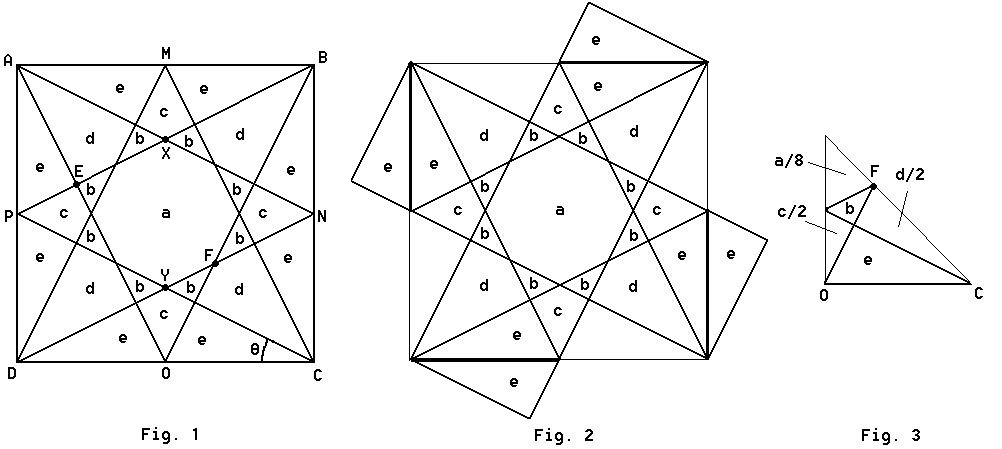
The first step is to draw the diagram. You can see this in Figure 1 of the picture. I've labeled each of the regions in the diagram because it's easier to represent things as variables this way. Notice that if some of the 'e' regions are moved around the figure can be transformed into Figure 2, which will become very useful soon. For the first part of the problem, it's pretty obvious, even with all of the lines drawn in, that the center square's area is 1/5. We can use bullet points for the steps in the second part's solution, which is a bit harder:
- Look at triangle ABE for a second; you'll notice that it's a right-angle triangle with a side ratio AE:BE = 1:2 (because of similar triangles). The area of such a triangle is AE2, and the hypotenuse is AE Sqrt(5), so if the hypotenuse is 1 the area is 1/5. But since the area of ABP is 1/4 (this is quite easy to see), and ABE + AEP (which is 'e') = ABP, the area of all 'e' blocks is 1/20.
- Next, we'll investigate triangle ABX. Lines AN and BP are diagonals of the rectangle ABNP, so the area of ABX is 1/4 of the area of that rectangle, or 1/8. Since 2e + c = 1/8, c = 1/40.
- Look at Figure 3, which represents an eighth of Figure 1 (remember, it's symmetrical). Now, to find the area of d simply, we can just find the area of triangle CFO, which will be easy if we can find out what CF is. If you look at Figure 2, you can see that, actually, the line CA traverses three equal squares, and so CF must be (CA)/3 = Sqrt(2)/3. Now we can find d: the area of CFO is (1/2)(CO)(CF)(sin FCO) = (1/2)(1/2)(Sqrt(2)/3)(Sqrt(2)/2) = 1/12, and then d/2 = 1/12 - 1/20 = 1/30, so d = 1/15.
- Finally, everything falls into place. ABP = 1/4 = 3*(1/20) + 1/15 + 1/40 + b, so b = 1/120.
- And, the central square of Figure 2 is 1/5 = a + 4b = a + 4*(1/120), so a = 1/6.
The final area list: a = 1/6; b = 1/120; c = 1/40; d = 1/15; e = 1/20.
There are some weird things going on here... notice that all of the sections' areas are the whole square's area divided by an integer? There are a lot of multi-section areas that behave like this too; for example, BNF = e+c+b = 1/12. Isn't that weird? Also, the transformation from Figure 1 into Figure 2 can help explain why this cross pentomino tesselates the plane. And finally, there are some great origami applications of this, which I'll leave you to figure out... Definately worth looking at. I love this problem.