Rubik's Cube Mechanics

Understanding the Cube

This page is about understanding the Rubik's Cube. If you want to be able to solve the Cube, talk about the Cube, or examine the Cube, it is necessary to understand - and be familiar with - its underlying mechanics, basic mathematics, and notation. There are too many people out there who try to solve the Cube but can't get anywhere because they do not take the time to look at it and understand how it works, and this page can teach you how to solve the Cube.

The Pieces of the Cube

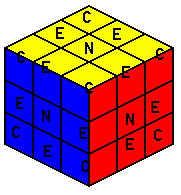
The Rubik's Cube is made of 26 visible pieces and one center spindle holding some of them together. There are 54 stickers, but thinking about stickers is the wrong way to go, because the stickers on an individual piece always stay together. There are three kind of visible pieces: center pieces (marked 'N') with one sticker each, edge pieces ('E') with two stickers each, and corner pieces ('C') with three stickers each.

First off, we will look at center pieces. There are six center pieces on a standard Rubik's Cube, each of which has a separate color. The center spindle holds these center pieces together in a fixed way, so that the centers can rotate but not change places. This means that the center pieces will always be in the same place relative to each other, so if you see the red and yellow centers next to each other, it will always be possible to hold the cube so that the red center is on top and the yellow center is at the front. Realizing that the centers are fixed is probably the most important first step to understanding the cube.

Next, let's look at edge pieces. There are twelve edge pieces on a Rubik's Cube, although you can only see nine in this diagram. Each edge piece has two stickers, and these two stickers are always from adjacent centers. No two opposite colors can ever be on the same edge. An edge has two orientations, which means that there are two ways it can be placed in each spot. Thus, it's possible for an edge to be in the right place, but misoriented ("flipped").

Finally, let's look at corner pieces. There are eight corner pieces, and you can see seven in this diagram. Each corner piece has three stickers on it, and the centers of these three colors are all next to each other on the cube. Like edges, no two opposite colors can ever be on the same corner. A corner has three different orientations, so even if it's in the right place, it may be misoriented ("twisted").

The pieces in a Rubik's Cube are organized into three layers (in each of the three directions). The vertical layers are often referred to as the first layer, second layer, and last layer.

Turns

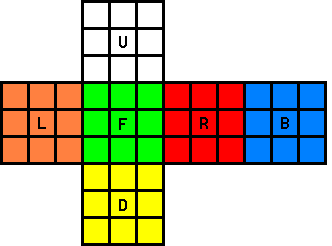
Any manipulation of the cube that changes the relative locations of pieces is called a turn. At the simplest level, each turn can be thought of as a rotation of one of the layers by some multiple of 90 degrees. You can see a description of how turns are written at the notation page. It's common to refer to faces by the letter that corresponds to a turn of that face. The F face, for example, is always the face closest to you, and the U face is always the uppermost face.

Perform a turn such as R'. Notice that this turn affects four corners and four edges, as well as rotating a center piece. On most Rubik's Cubes, you will not have to keep track of the centers' rotations, but in some cubes you will have to, because a twisted center will look wrong. In these cases, centers have four orientations.

For more on sequences of turns, look at the commutator page.

Describing Pieces

It's common to describe pieces by the faces, or layers, that they lie on. A center would be called by one letter (such as U), an edge by two letters (such as UF), and a corner by three letters (such as UFR). On bigger cubes, people will often describe each layer the piece is on, using an uppercase letter for the shallowest layer, a lowercase letter for the next layer, and M, E, or S for the middle layer. For instance, on the 4x4x4, an edge might be referred to as UFr.

The Cube as a Physical Object

Although the Rubik's Cube is often described as a mathematical construct - this is used whenever we talk about move sequences and turns, for example - it is also a physical object. This has a number of implications.

First, you can solve the Cube for speed, because you can learn to make turns very quickly. Top solvers can get as high as 8ish turns per second over a full solve. In the very early days of the cube, almost everyone turned with their wrists, but nowadays people make turns with the push of a single finger. Using techniques called fingertricks, it's even possible to do two or three moves in one motion. Youtube has many great examples of these.

Second, some Rubik's Cubes may squeak when turning or may be difficult to turn. This is especially common with official Rubik's brand cubes; the best cubes, with carefully designed mechanisms and adjustable tension, come from special companies in Asia. If your cube is hard to turn, an easy and quick solution is to lubricate it. In the cubing community, silicone spray and oil are considered the best lubricants, because they work well and don't degrade the cube. There are even some specialized sprays for cubing, such as Lubix and Maru lube. I really don't recommend trying other common household lubricants, such as WD-40 or Vaseline - go with what's proven to work.

Finally, Cubes are subject to deterioration. The plastic tends to wear down with time, leaving small bits of plastic dust inside the mechanism, and although you can clean that out, every cube will get looser with age. At some point the only solution is to buy a new one. The stickers will wear down too (especially if they are the official Rubik's type, or if you have a habit of removing them), but they can be replaced much more easily. I recommend using Cubesmith for all replacement stickers - they are high-quality and resist deterioration for a long time, and they provide stickers for a large number of different puzzles.

Mechanics of Higher-Order Cubes

The 3x3x3 is not the only Rubik's Cube that you can buy. In fact, cubes from 2x2x2 through 7x7x7 can be bought, and there are a few knockoff or limited-edition samples of even higher-order cubes. These larger cubes are a lot more complicated (and interesting!).

In general larger cubes have more pieces and turnable layers. In a 5x5x5 cube, for instance, there are five turnable layers on each axis, and there are 98 visible pieces (plus one center spindle). The 5x5x5 has 9 centers for each one on the 3x3x3, and 3 edges for each one on the 3x3x3, but the number of corners is unchnged.

One interesting thing about large cubes is the interchangeable centers. For each type of centers (not counting ones that are attached to the center spindle), there are four pieces of each of the six colors, so you can change some of these pieces around and still have a solved cube. It turns out that, although the 3x3x3 is a great example of a mathematical group, larger cubes aren't groups at all.

The fastest solution method for the larger cubes is to pair up pieces until it resembles a 3x3x3, and then solve that. On even cubes, the centers aren't fixed like the 3x3x3, and so it's possible to end up with positions that are impossible on the 3x3x3. You can flip a single edge, or swap two edges without affecting anything else. Unfortunately, the only way to fix this for good (without changing the method) is to learn some pretty lengthy move sequences.